New Forward Error Correction Codes

Thanks to the work of the last GSoC and the researchers at Virginia Tech, we now have an implementation of LDPC and turbo product code (TPC). These classes of codes have a number of possibilities for their setup and runtime behavior. LDPC in particular has a pretty good selection of techniques to compute them, and we're working on adding at least a second way of doing things -- again, coming from last year's GSoC projects.

GNU Radio contains a BER curve generator called ber_curve_gen.grc and installed as a gr-fec example. We can easily add new FEC codes to this test, the output of which is plotted below, truncated after some time so the curves haven't all been smoothed out, yet.

First, we're plotting BER vs Es/N0 and not Eb/N0, so this is showing performances at different code rates. The TPC and LDPC codes are using the default parameters, which could be improved upon. In fact, there is still probably lots to learn about all of this. In this case, the LDPC was using the default alist that comes with GNU Radio (found in gr-fec examples directory) and the only change from the default TPC encoder and decoder was to use the MAX LOG-MAP decoder.

To see the differences in just the TPC decoder modes available, I plotted all five against each other. These are the same codes and rates with just different approaches to decoding them. What was not analyzed here, however, is the computational cost of each, and I would suspect we'd see a direct trade-off between BER performance and required compute power.

And if you haven't seen the new FEC-API, this is a way to easily use encoders and decoders of varying styles and requirements in both streaming and bursty communications. It makes using and reusing FEC blocks very easy between GNU Radio applications as well as allows us to easily use and replace the FEC being used in any given application. GNU Radio installs many examples for how to use the encoders and decoders in streaming, tagged stream, and PDU message modes into the digital examples directory.

Finally, these codes are not greatly optimized for speed. We felt it was important to provide access to the codes now so they can start being utilized in real systems. Hopefully, this is intriguing enough that one or more serious coders takes this as an opportunity to improve things.

What's the right way to calculate tanh?

I'm working on improving the synchronization of M-PSK phase-locked loops, which we call the Costas loop in GNU Radio. I'll post later about what I'm doing and why, but the results are looking very satisfying. However, during this work, I need to calculate a tanh. In my simulation proving the algorithm, I did it all in Python and wasn't concerned about speed. Moving this to a GNU Radio block and the thought of calling a trigonometric function from libm gave me chills. So I thought that I'd look into faster approximations of the tanh function.

Spoiler alert: this is a lesson in optimization and never trusting your gut. The standard C version of tanh is amazingly fast these days and the recommended function to use.

So what are our options for calculating a tanh? I'll go through four here, some of which I had help from the #gnuradio IRC chatroom to explore.

1. Calling tanhf(beta) straight from libm.
2. Calculating from an exponential: (expf(2*beta)+1) / (expf(2*beta)-1)
3. Using a look-up table (LUT)
4. An expansion approximation from stackexchange (the last equation from July 18, 2013)

There are, I'm sure, other algorithms that will calculate a tanh. I know that we can use the CORDIC algorithm in hyperbolic mode, though my tests of the CORDIC algorithm, while appropriate in hardware, are not good in software. However, we'll see that we don't really need to go to great lengths here before we can be satisfied.

The code I used to test is rather simple. I time using GNU Radio's high_res_timer to get the start and end time  of a loop. The loop itself runs for N floating point samples, and each input sample is calculated using the standard random() function. I want to make sure each number into the function under test is different so we don't benefit from caching. Just putting in 0's makes the test run almost instantaneously, because of the known special case that tanh(0) is 0.

Within each loop iteration, it calculates a new value of beta, the input sample, and one of the four methods listed above. The tests are performed on an Intel i7 870 processor running at 2.93 GHz as well as an ARMv7 Cortex-A9 (using an Odroid-U3) at 1.7 GHz. Tests were run with 100 million floats and compiled using G++ with -O3 optimization. Download the code here.

Results 1

In the following tables of results, the "none" category is the baseline for just calculating the random samples for beta; there is no tanh calculation involved. All values are in seconds.

Intel i7 870

• none: 0.682541
• libm: 0.700341
• lut:  0.93626
• expf: 0.764546
• series approx:  1.39389

ARMv7 Cortex-A9

• none: 6.12575
• libm: 6.12661
• lut:  8.55903
• expf: 7.3092
• series approx: 8.71788

Results 2

I realized after collecting the data that each of the three methods I developed, the LUT, exponential, and series approximation method were all done as function calls. I'm not sure how well the compiler might do with inlining each of these, so I decided to inline each function myself and see how that changed the results.

Intel i7 870

• none: 0.682541
• libm: 0.700341
• lut:  0.720641
• expf: 0.81447
• series approx:  0.695086

ARMv7 Cortex-A9

• none: 6.12575
• libm: 6.12661
• lut:  6.12733
• expf: 7.31014
• series approx:  6.12655

Discussion

The inlined results are much better. Each of the approximation methods now starts to give us some decent results. The LUT is only 256 values, so the approximation is off by up to about 0.01 for different inputs, and it still doesn't actually beat libm's implementation. Calculating with expf was never going to work, though it is surprisingly not bad for having that divide in it. Raw comparisons show that libm's expf is actually just by itself slower than tanh, so we were never going to get a win here.

Finally, the series approximation that we use here is pretty close, maybe even somewhat faster. I didn't run these multiple times to get an average or minimum, though, so we can only say that this value is on par with the libm version. I also haven't looked at how far off the approximation is because the libm version is so fast comparatively that I don't see the need, and this is true for both Intel and ARM processors.

I'm surprised, though pleasantly so, that for all of this work, we find that the standard C library implementation of the "float tanhf(float x)" function is about as fast as we can expect. On an Intel processor, we computed 100 million floats, which added 17.8ms to the calculation of just the random numbers, which means that each tanh calculation only took 178 ps to compute. I actually have a hard time wrapping my head around that number. I'm sure that the compiler is doing some serious loop optimization seeing as this is the only thing going on inside here. Still, until I see this being a problem inside of a real algorithm, I'm satisfied with the performance to just use the standard C library's tanhf function.

Further Discussion

One of the big problems with benchmarking and providing results for general purpose processors is that you know that the results are so directly tied to your processor version and generation. Using a Macbook Pro from 2014 with a newer i7 processor gave similar relative results but with much better speeds, even though it only runs at 2.6 GHz instead of 2.93 GHz. But that's technology for you. The important lesson here is that the processor and compiler designers are doing some tremendous work making functions we used to never even think about using wonderfully fast.

But the other thing to note is that YMMV. It used to be common knowledge that we want to use look-up tables wherever possible with GPPs. That seems to have been true once, but the processor technology has improved so much over memory and bus speeds that any memory access, even from cache, is too slow. But this means that if you are running an older processor, you might suffer a bit extra based on these results off more current computers (then again, the Intel tests are from a processor that's roughly three years old). What is really noteworthy is that the ARM showed similar trends with the results, meaning we don't have to think about doing anything differently between ARM and Intel platforms. Still, you might want to bechmark your own system, just in case.

We could also think about using VOLK to code up each of these methods and let the VOLK profiler take care of finding the right solution. I'm against this right now only in that we don't have good measurements or even concerns about the approximations, like with the LUT method. We are not only trading off speed, but also a huge amount of accuracy. In my application, I wasn't concerned about that level of accuracy, but VOLK will and should for other applications.

Finally, one thing that I didn't test much is compiler flags. The tests above used -O3 for everything, but the only other setting I tested was using the new -Ofast, which also applies the -ffast-math. I found that some versions of the algorithm improved in speed by about 10ms and others reduced in speed by about 10ms. So it didn't do a whole lot for us in this instance. There may, of course, be other flags that we could look into for more gains. Similar mixed results were found using Clang's C++ compiler.

I'd like to thank Brian Padalino, Macus Leech, Tim O'Shea, and Rick Farina for chatting about this on IRC and poking me with new and different things to try.

Update on 2014-09-02 14:15 by Tom Rondeau

Brian Padalino got back to me this morning after having similar trouble with the fact that it looked like tanh was being computed in picoseconds, except he went and did something about it. I thought that by recalculating a random result for beta in every iteration of the loop that I was preventing anything from caching, since the tanh functions would always have to operate on a new value. However, I'm guessing that if I looked into and parsed the assembly output for my code, I would see some optimizations related to the fact that the loops were just getting a new random number and calling the tanh functions on it. There was definitely some optimizations happening here that were not helpful to us understanding these calculations in a real-world piece of code.

Instead, Brian added the C/C++ keyword volatile to the x, y, and z variables in the code. This prevents the compilers from optimizing the use of these variables, which means that whatever cleverness was happening above wouldn't anymore. The numbers now start to look much more reasonable from our expectations. But also, I assume, more reasonable in how the tanh function would really be called in our applications.

This is a really good lesson for me since I've struggled with this concept of benchmarking code like this and worrying about over-optimization by the compiler. So the new results are:

Intel i7 870

• none: 0.774824
• libm: 4.94122
• lut: 0.92123
• expf: 2.48623
• series approx: 1.61947

ARMv7 Cortex-A9

• none: 6.72212
• libm: 19.2388
• lut: 8.88899
• expf: 17.2966
• series approx: 10.8309 

So the LUT and series approximation make a big difference now. Somewhat disappointing to see this after yesterday's post, but I believe these numbers are more representative.

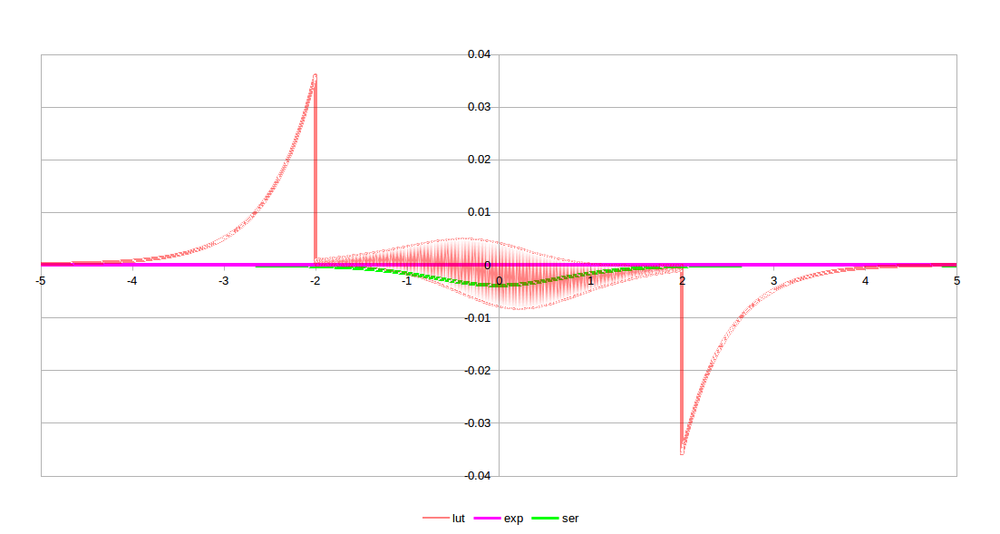
Approximation Error

Let's now look at how good each of these approximations are. The mean difference between the approximations and the standard tanh are: 

• lut: 0.00317092
• exp: 1.53656e-8
• ser: 2.48358e-8

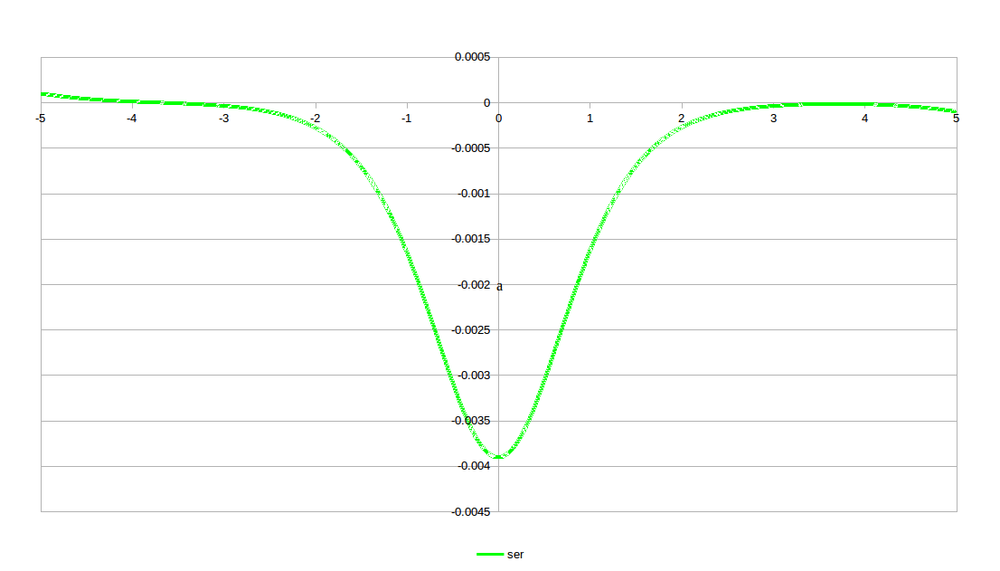
 As expected, the LUT performs the worst since it wasn't designed with any high accuracy, and the series approximation is very, very good. It should come as no surprise that the exponential equation is as good as it is since it's just an alternative form of the tanh.

And below is what the errors look like. Again, not surprisingly, the LUT version dominates the errors. And since the LUT was somewhat arbitrarily kept between -2 and +2, the discontinuity there is expected. For the application I have in mind, the values should be within this range, anyways. A look at just the series approximation is shown as well so we can just see that one.